Définitions
Intuitivement, un réseau d'automates est un ensemble
d'éléments en interaction.
On représente le temps par un
entier naturel:
t =
{0,1,2,3,.........,n,.........}
Automates d'états finis.

Un automate au sens de l'informatique.
En informatique, un automate est
défini par la donnée de trois ensembles discrets:
I, l'ensemble des entrées i,
S, l'ensemble des états internes s,
et O, l'ensemble des sorties o,
ainsi que par deux applications:
S (i,s), la fonction de changement d'état nouvel état au temps t+1 en
fonction de l'entrée et de l'état au temps t,
et O(i,s),
la fonction de sortie sortie au temps t+1 en fonction de
l'entrée et de l'état au temps t
Les
entrées, les états internes et les sorties peuvent
être multiples .
Le nombre des entrées
d'un automate k s'appelle la
connectivité d'entrée
de l'automate.
Définition simplifiée
Nous ne considéront que des automates dont l'état
interne et la sortie sont identiques.
Un automate simplifié sera donc défini par:
- ses ensembles d'entrées et de sorties,
- la fonction de transition donnant la
sortie au temps t+1 en fonction des entrées au temps t.
De plus, nous nous limiterons aux
automates binaires, c'est-à-dire à deux états, par
exemple 0 et 1.
Exemple: les automates booléens
Les automates booléens
opèrent sur des variables binaires, c'est-à-dire dont les
valeurs sont 0 ou 1 (FAUX ou VRAI).
Exemples: les fonctions logiques habituelles ET, OU, OU exclusif.
Tables de vérité
de quatre fonctions logiques booléennes à 2
entrées:
ET OU OU
exclusif NON-ET
Entrées 00 01 10 11 00 01 10 11 00 01 10 11 00 01 10 11
Sortie 0 0 0 1
0 1 1 1
0 1 1 0 1 1 1 0
Un automate booléen à k
entrées, dit de connectivité k,
est défini par une table de vérité donnant
l'état de la sortie pour chacune des 2k configurations
d'entrée.
Nombre d'automates booléens de connectivité k:
2 à la puissance 2k
.
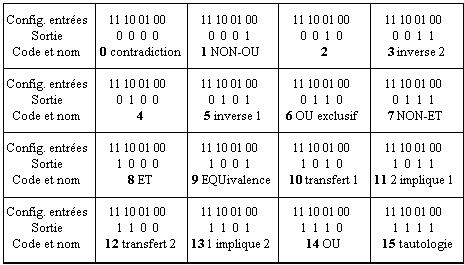
Les
seize fonctions booléennes à deux entrées,
définies par leurs tables de vérité.
RESEAUX D'AUTOMATES
Propriétés structurelles
Un réseau
d'automates est:
un ensemble d'automates reliés entre eux de telle sorte
que les sorties des uns soient les entrées des autres.
C'est donc un graphe orienté:
- les nœuds sont les automates;
- les arêtes les connexions dirigées de la
sortie d'un automate vers l'entrée d'un autre.
Un
réseau de cinq automates booléens à deux
entrées, cinq relations logiques:
e(1) = OUex ( e(2) , e(3) )
e(2) = EQU ( e(3) , e(4) )
e(3) = ET ( e(4) , e(5) )
e(4) = EQU( e(5) , e(1) )
e(5) = OUex ( e(1) , e(2) )

Structures
de connexions
On est amené à
considérer des structures de connexions variées.
- Les règles de connexion peuvent avoir un
caractère aléatoire; dans ce cas la définition des
entrées ne peut se faire que par la liste exhaustive des
entrées de chaque automate: on parle alors de connectivité
aléatoire.
- Nous serons aussi conduit à étudier le cas
où chaque automate est connecté à tous les autres: la connectivité est alors complète.
- Enfin, la connectivité cellulaire
présente un grand intérêt théorique et
pratique: les automates sont répartis sur un réseau de
petite dimensionnalité (1, 2 ou 3) et les connexions se font
entre proches voisins (voir les deux chapitres suivants sur les
automates cellulaires).
- Petits mondes: beaucoup de connexions cellulaires,
plus quelques connexions aléatoires.
- Réseaux invariants d'échelle:
connectivité très variable variable. P(k)= (1/k)a
Propriétés dynamiques
La dynamique d'un réseau
d'automates est entièrement définie par:
- le graphe des connexions,
- les fonctions de transition des automates
itération parallèle: dans ce mode, tous
les automates changent d'état en même temps en fonction de
l'état des automates d'entrée au temps
précédent:
itération séquentielle:
un seul automate à la fois change d'état.
plus
toutes les variantes.
Graphe
d'itération
L'ensemble des états d'un
réseau de N automates booléens
comprend donc 2N
configurations possibles.
On passe d'une configuration à une autre en appliquant la
règle de changement d'état à chaque automate.
La dynamique est donc entièrement décrite par le tableau
des successeurs.
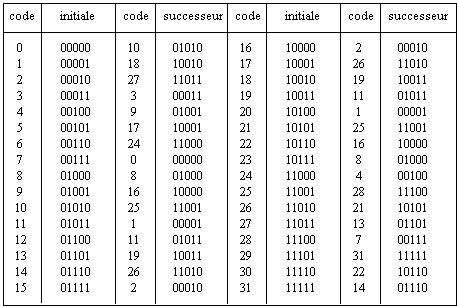
Tableau 2.2. Tableau des successeurs. Dans la
partie droite de chaque demi-tableau, figurent les configurations
binaires et les codes décimaux des successeurs des 32
configurations initiales figurant à gauche, obtenus après
une itération parallèle par le réseau de la figure
2.4 .
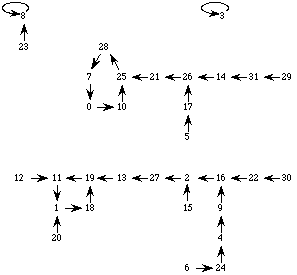
A partir de ce tableau on peut tracer un graphe orienté, le graphe
d'itération:
- les noeuds sont les configurations du
réseau,
- les arêtes orientées indiquent le sens des
transitions d'une configuration du réseau au temps t à la
configuration au temps suivant t+1.
Attracteurs
Un
réseau d'automates est un système déterministe: si
le réseau passe une deuxième fois par une configuration
précédemment atteinte, la suite des états
parcourus après le second passage est la même
qu'après le premier .
Le système décrit donc indéfiniment une boucle
dans l'espace des états.
- Ces boucles s'appellent les attracteurs;
- le temps de parcours de la boucle, la période
de l'attracteur.
- Si cette période est 1, l'attracteur est un
point fixe.
- On parle de cycle limite si la période
est supérieure à 1.
- L'ensemble des configurations évoluant vers un
attracteur donné constitue un bassin d'attraction.
Pour les réseaux de grande
taille on détermine:
• le
nombre des différents attracteurs,
• leurs
périodes,
• la
taille des bassins d'attraction (le nombre des configurations qui
évoluent vers l'attracteur),
• la
durée des transitoires (c'est-à-dire le temps
d'évolution depuis les jardins d'Eden, configurations sans
prédécesseurs, jusqu'à l'attracteur).
La distance de Hamming entre
deux configurations quelconques est le nombre des automates dans des
états différents.
Les lois d'échelles reliant
par exemple le nombre et la période des attracteurs au nombre
des automates sont des propriétés
génériques de la dynamique.
Boucles
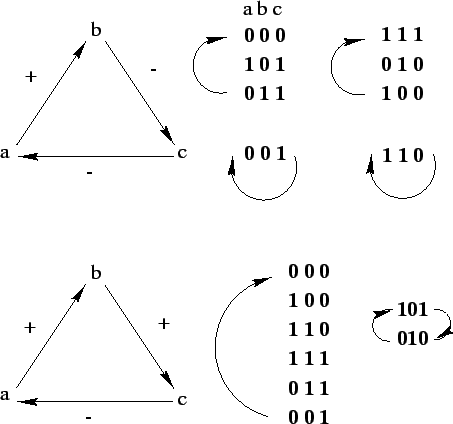
Figure 1: Réseaux en boucle formés de trois
automates à une entrée. A droite, les deux réseaux
sont composés d'éléments simples qui transmettent
le signal d'entrée (signe +) ou l'inversent (signe -). A gauche
sont représentés les graphes d'itération des
réseaux correspondants. Le graphes d'itération du
réseau du haut non frustré, comprend quatre cycles dont
deux configurations stables. Celui du bas correspondant à une
boucle frustrée, comprend un "long" cycle de six configurations
et un cycle court de période 2
 |
Un cas simple: les
"crabes"
Réseaux d'automates à une seule entrée.
Les
différents automates booléens à une seule
entrée sont au nombre de quatre:
- deux sont invariant , l'un à 0, l'autre à 1.
- deux autres transmettent le signal, resp. avec ou sans
inversion, resp. - et + .
Structuré
en sous-réseaux indépendants:
Chaque sous-réseau comprend une boucle d'où sont issues
des branches par lesquelles s'écoule le signal issu des boucles.
Le signal ne peut entrer dans une boucle, car le nœud par lequel il
rentrerait aurait alors deux entrées, une interne à la
boucle, l'autre externe.
C'est aussi la raison pour laquelle un sous-réseau ne comprend
qu'une boucle:
le sens de propagation le long d'une branche est défini par la
boucle dont elle est issue; deux boucles ne peuvent donc pas être
reliées par une branche.
D'une manière imagée nous appellerons "crabes" les
sous-réseaux,
"têtes" les boucles et "pattes" les branches issues des
têtes.
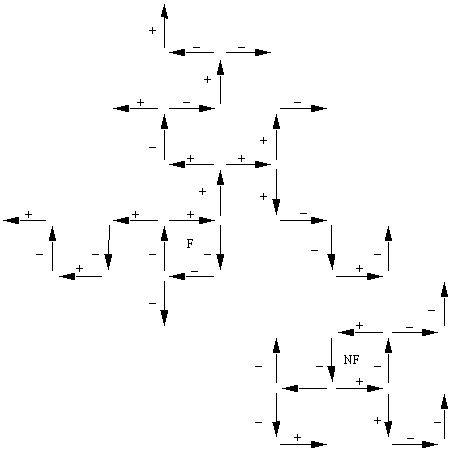
La dynamique des
états d'une patte correspond à la propagation d'un signal
de l'entrée du premier automate vers le dernier automate de la
patte.
A l'instant t,
l'état du i-ième automate de la patte ne dépend
que de l'état du premier automate de la patte au temps t-i. Si
l'on part d'une configuration initiale quelconque, le transitoire ne
subsiste que tant que le signal provenant de la configuration initiale
se propage le long des pattes.
Dans le régime permanent qui est celui des attracteurs, le
signal se propageant le long des pattes est celui issu de la tête
du crabe.
La longueur maximum du transitoire est donc celle de la plus longue
patte du crabe.
Par la suite, tout est déterminé par la boucle de la
tête. La période du crabe est donc celle de sa tête.
Deux cas se présentent, suivant que le crabe est frustré
ou non.
L'étude théorique permet donc de déterminer la
dynamique des réseaux booléens à une entrée
:
- la longueur du transitoire,
- la période des attracteurs (PPCM des périodes
des crabes indépendants)
- le nombre des attracteurs (c'est le produit du nombre des
attracteurs de chacun des crabes;
- La taille des bassins d'attraction: c'est le produit de la
période par 2p,
où p est le nombre total des automates des bras.






